To explain those algoritms, it is good to first make definitions.
To create a picture of a fractal, you must give every pixel a color. This is done by scanning all pixels. It make no sense on which order you are selecting pixels. Every pixel is undependent of each other. (Of course you can merge pixels by mixing colors of a small square of pixels into one new pixel, but this is done after these pixels are already scanned.)
When filling a pixel with a color, you start a Walk. This starting point is the point that belongs to the pixel. A point in this algoritm is by definition a complex value, so the starting point is also a complex value: Z0.
When a point (a complex value) is put into the formula, the result is also a complex value. The point is taking a Step: Zn -> Zn+1.
You can make so many steps as you like, but (as every walk) you must stop at a time. This finit list of Steps is called a "Walk".
If a Walk take n steps, you can write it as: Z0->Z1->Z2->....Zn-1->Zn
When drawing a fractal, you always take a piece (rectangle) of a complex space, in which the fractal is present. This rectangle piece is a Viewport. When the Viewport is great, for example (-2,-2) - (2,2), the whole fractal is visible (when using a kwadratic formula z -> z2 + c), but when it is small (0.5,0.2)-(0.5000001,0.2000001), you can zooming into a piece of a fractal, so that part is enlarged a million times!
If you have for example a resolution of 1000 times 1000 and a Viewport of (1.0, 0.2) - (1.1, 0.3).
You must map the viewport onto the pixels, before you can draw the fractal.
By convention, the real part of complex values is mapped horizonally (x) from low at left to high at right,
and the imaginair part of complex values is mapped vertically (y) from low at bottom to high at top.
So, in this case, you create a convertionally oriënted fractal by do the mapping as follows:
- Map the upper-left pixel at (1.0, 0.3)
- Map the upper-right pixel at (1.1, 0.3)
- Map the bottom-left pixel at (1.0, 0.2)
- Map the bottom-right pixel at (1.1, 0.2)
You can mirror the picture of a fractal by swithing the mapping with left/right or top/bottom.
A piece of the two dimensional space of the fractal is selected to draw on the screen.
For Julia fractals using a quadratic functions as z' = z2 + c, the fractal always fits in the ractangle from (-2,-2) to (2,2).
You can zoom (extremely) in by taking a very small rectangle, for example (1.344, -0.750) - (1.345, -0.749)
resulting in a magnification of about 1000.
To fill in the selected reactangle, every pixel (x,y) of the rectangle is taken belonging the complex value z0 = x + iy. It is the Starting Point.


When you take a complex value zn and put it through a certain complex function, you get a new value zn+1. That is a "Step".
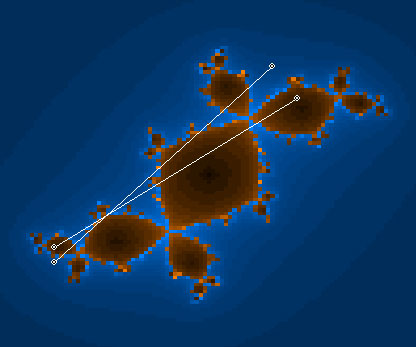
When you put again zn+1 into the function, you get zn+2, etcetera.
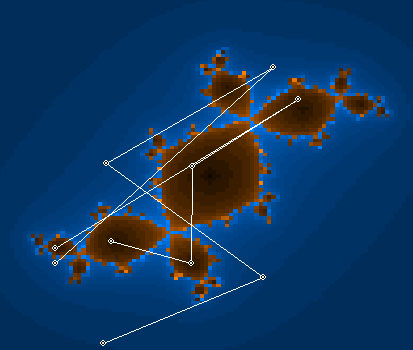
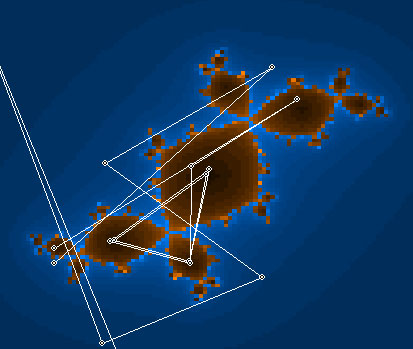
Repeating taking steps create a "Walk".
When the "Walk" goes away from the center, the distance of (0,0) becomes greater and greater, the point z goes towards the infinit attractor.
You can define "nearby" a infinite attractor as follows:
z*x,y) is "nearby" when x2 + y2 > r, with r of a high number (h).
When you draw a great circel of radius 1000, and define "nearby" when entering the ouside part of a circles, then the value of h is 1,000,000.
When the steps of the "walk" grows smaller and smaller, the point z goes towards a finite attractor.
You can define "nearby" a infinite attractor as follows:
z is "nearby" when the distance of zn and zn-1 is smaller than a small number s. For example 0.0001
In the Julia algoritm, To display the fractal, for every pixel z0 the length of a "walk" of each starting point is calculated until xn is "nearby" an attractor.
when for example it takes 7 iteration to get z "nearby" a infinite attractor, the value 7 is mapped into a color (for example using a color palette)
when for example it takes 13 iteration to get z "nearby" a finite attractor, the value 13 is mapped into a color (for example using a (alternate) color palette)
Sometime it will take too long to get zn nearby an attractor, so a maximum of iteration is defined. When for a pixel z the maximum is reached, you give that pixel a choosen color.
In the Julia algoritm, the same function (using the same constants) is used for all complex value of each pixels.
For example when using zn+1 = zn2 + c, with c = 0.2 + 0.3i, it is applied to all pixels.
In the Mandelbrot algoritm, the complex value of the starting point of the "walk" is used as a constant of the complex function.
For example when using zn+1 = zn2 + z0, it is applied to the complete "walk" from the pixel z0.